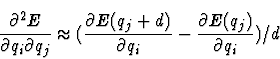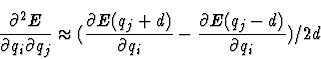


Next: Implementation
Up: The Free Format Section
Previous: Control of constraints
Calculation of the Hesse-Matrix
There are two keywords (HESSE and SELHESSE) which control the
calculation of the cartesian force constant Hesse-Matrix.
Such a Hesse-Matrix can be used later to calculate a IR vibrational spectrum.
The approximation of the Hesse-Matrix
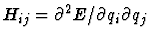 is done by finite differences of the first derivatives of the total energy E.
This is either done via a one point approximation
is done by finite differences of the first derivatives of the total energy E.
This is either done via a one point approximation
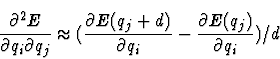
or a two point approximation
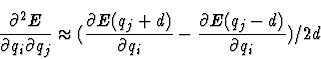
, whereas d denotes the step-length of each finite differene step in x, y and z
direction.
With the keyword HESSE one can select between one of the two modes
and set the step length given in Å. The keyword SELHESSE is
manditatory and is used to specify a set of atoms for which the
Hesse-Matrix should be calculated. Example:
HESSE 2 0.01
SELHESSE A*
In that example all atoms are selected for the calculation of the Hesse-Matrix.
The calculation is done by the two point approximation and uses a step length
of 0.01Å.
In the output-directory of EGO the file hesse.out is created with the
corresponding Hesse-Matrix. The dimension of the elements in the Hesse-Matrix is
N/m. In the util-directory there is the utiliy program hess2hess which
is able to convert such a Hesse-Matrix to other formats and dimensions.
Note: Features which will affect the proper calculation of the Hesse-Matrix,
like, e.g., Minimization, Equilibration or SHAKE are automatically switched off.
Furthermore, the number of steps necessary to perform the calculation of the
Hesse-Matrix is set automatically.
The Hesse-Matrix is stored in the file hesse.out.
The header of that contains the atoms with their masses and positions.
So, if you like to investigate isotipoc effects you just have to
change the masses here in the file. After the keyword Matrix the hesse-matrix follows.
Note: If you choose many atoms
for a hesse-calulation the lines in that file get very long and
some ASCII editors (like the good old vi will not work properly and
will destroy the file).
It is also possible to restart a hesse calculation. Just restart again normally.
EGO will look in the hesse.out file and will see how far it
is. If it is not completed it will restart at the right point.
EGO recognizes the status of the hesse-calcualtion from two numbers
in the first line after the number of atoms.
If it is not completed there will be for example
3 1 2
The first number specifies the number of atoms for which the
hesse matrix should be calulated.
The second number specifies the atom which is currently is moved and
the third number specifies in which direction it is moved.
Once it is completed only the number of atoms will be left.
Example for a completed hesse-matrix for H2O:
3
1 OH2 15.99940 -0.60543 0.00000 0.77339
2 H1 1.00800 0.00000 0.00000 1.54678
3 H2 1.00800 0.00000 0.00000 0.00000
Matrix:
620.76339 0.00555 0.12451 -302.92413 0.00365 -255.71554 -302.90517 0.00985 255.72955
1.34366 -18.29916 -0.03854 -0.53269 -2.53697 -0.13334 -0.52906 -2.54235 0.14224
-0.26595 -3.61815 867.78234 -346.08646 -0.31560 -440.00671 346.51745 -0.77901 -440.35201
-306.01033 0.02860 -349.09602 287.57882 0.00321 300.09174 15.91631 -0.01153 44.18106
4.88112 25.75767 -1.80326 1.59560 3.98306 0.36573 -0.07680 -3.65888 -0.43499
-256.41766 0.18216 -426.99687 301.58252 0.77197 486.95572 -45.46118 -1.13272 -46.69626
-306.92754 0.00193 359.79018 15.84619 0.01383 -43.98345 288.33121 -0.01516 -300.36040
4.50220 23.25857 1.67851 -0.02868 -2.56054 0.52004 1.64183 3.16829 -0.43899
256.58000 1.09238 -426.33925 45.55342 -0.96294 -46.79383 -301.54461 0.63691 487.03730



Next: Implementation
Up: The Free Format Section
Previous: Control of constraints
Helmut Heller
2000-04-19