


Next: Multiple Time Step Method
Up: Methods to Increase Efficiency
Previous: Methods to Increase Efficiency
Distance Cut-Off Scheme
The most commonly used approximation cuts-off all pair interactions beyond a
certain maximum distance
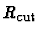 .
The cut-off is achieved by multiplying the force by a `cut-off'-function,
which depends only on the distance and
reduces the force to zero in a continous, differentiable,
manner. A typical `cut-off'-function assumes the constant value unity
up to a distance
.
The cut-off is achieved by multiplying the force by a `cut-off'-function,
which depends only on the distance and
reduces the force to zero in a continous, differentiable,
manner. A typical `cut-off'-function assumes the constant value unity
up to a distance
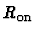 , then decreases to zero
between
, then decreases to zero
between
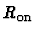 and
and
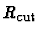 and remains zero for
all distances greater
than
and remains zero for
all distances greater
than
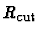 . As a result, only interactions up to the
distance
. As a result, only interactions up to the
distance
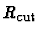 have to be evaluated.
have to be evaluated.
The appropriate choice of
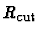 is a compromise between
accuracy and computing time. On the one hand, the smaller
is a compromise between
accuracy and computing time. On the one hand, the smaller
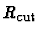 is chosen, the faster the computation will be
carried out.
On the other hand, a large
is chosen, the faster the computation will be
carried out.
On the other hand, a large
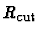 will reduce the error
of the approximation.
will reduce the error
of the approximation.
The `cut-off', although often employed, cannot be an appropriate
approximation for molecular dynamics simulations since a neglect of the Coulomb interaction is believed to
cause major rearrangements within the molecule.
An improved approximation scheme involves ordering of the long-range
interactions according to distance classes [44], as described
below. A similar algorithm had been suggested in [37] for
short-range forces in Lenard-Jones liquids.



Next: Multiple Time Step Method
Up: Methods to Increase Efficiency
Previous: Methods to Increase Efficiency
Helmut Heller
2000-04-19
![]() is a compromise between
accuracy and computing time. On the one hand, the smaller
is a compromise between
accuracy and computing time. On the one hand, the smaller
![]() is chosen, the faster the computation will be
carried out.
On the other hand, a large
is chosen, the faster the computation will be
carried out.
On the other hand, a large
![]() will reduce the error
of the approximation.
will reduce the error
of the approximation.