A sample application

Assume we want to predict the gating reaction of gramicidin A, a small ion channel. The initial structure entered into the flooding simulation described below is depicted in Fig. 6.6 (upper two panels); the predicted final configuration is depicted in Fig. 6.6 (lower two panels). Water molecules are drawn in blue. Note the red (dark) ring, which has moved outside the channel to enable the passage of ions through the channel. This gating has been observed by patch clamp measurements.

 

For the flooding simulation we proceed as follows:

Steps 1 and 2:
We assume an equilibrated structure (gram.pdb and gram.psf) is available, which does not show considerable conformational motions within nanoseconds. In particular, no gating transition is observed on that time scale. The system contains a total of 353 atoms. The necessary *.lis-files are available or have been created with xpl2lis and, eventually, with mkmaxw.

Steps 3 and 4:
We perform an unperturbed MD-simulation of 300 picoseconds length to create an ensemble of structures, from which the flooding potential can be derived. For that purpose, coordinate files (ego-files) are written every 100 steps. A slight coupling to a heat bath (room temperature, $300\,$K) is used, and, very importantly, translation/rotation correction is switched on. To tell EGO which atoms to consider for the translation/rotation correction, we have to create a dummy flooding file flooding.lis first:

mkflood gram.pdb gram.PSF 0 0 0 0 0 'RDIOX ACA -R3 -R5 -R8 -R9 -R12'

Here, the selection string selects all atoms of the dioxilane ring (which has residue name DIOX in the pdb-file) as well as all alpha carbons of the backbone with several exceptions given explicitly to save computer time. This choice is motivated by the expectation that mainly the dioxilane ring and the protein backbone are actively involved in the gating conformational transition. This is not to say that all other atoms will not be allowed to move; it is just that the force driving the destabilization of the initial configuration will not act upon the unselected atoms.

The dummy flooding file can now be used by EGO to create the 300 picosecond ensemble. The following control file ctl.lis is used:

33              Number of files.
shake.lis               
coord.lis               
...
forceout.lis            
2               Requested number of nodes.
353             Number of atoms.
100             Freq. of analysis printout; next line is ...
A*
10              Frequency of writing restart file every analysis step!
0               Frequency of system call every analysis step.
ego2crd.sh
-5              Frequency of energy printout.
300000          Number of integration steps.
1e-15           Integration time step in s.
5               Order of exclusion list.
FALSE           Switch for Minimisation.
1               Friction factor (1.0=>no friction, 0.0=>no motion).
0.08            Maximum position movement per integration step in A.
TRUE            Switch for Equilibration.
300             Target temperature in Kelvin.
1e-12           Coupling time constant in s.
8               Number of distance classes.
...
0               Used type of cluster algorithm (0 is default).
-2              Number of hierarchy levels.
-18             Number of branches on last level.
500             Frequency of reclustering.
out/            Path for output data.
0.4             Scaling factor for special 1-4 electrostatic damping.
TRUE            Switch for stochastic boundary.
TRUE            Switch for harmonic restraints.
TRUE            Switch for SHAKE on hydrogens (Only bond length).
...
FALSE           Switch for using flooding.
TRUE            Switch for using transl/rotation correction.
FALSE           Switch for using adaptive flooding.
0               Initial energy for flooding in kT.
0               Final energy for flooding in kT.
0               Flooding energy increase in kT/ps.
1e-12           Time constant for adaptive flooding in s.
0 0             Number of user defined integers and doubles.
END
0               DEBUG: 1 == compare with exact forces
0               DEBUG: only should be used by a developer.

From the ensemble of 3000 structures (ego-files) we chose all except for the first 500 (which might be perturbed due to a non-relaxated initial structure) to create the flooding matrix with mkflood. We use extrapolation of the eigenvalues with a minimal number of 1000 structures and a total of 10 steps for the extrapolation. m=20degrees of freedom shall be `flooded':

mkflood gram.pdb gram.PSF 500 3000 1000 10 20 'RDIOX 
        ACA -R3 -R5 -R8 -R9 -R12'

Note that we used a selection string identical to the one used to create the dummy flooding file for the translation/rotation correction. This should always be done.

Steps 5 through 8:
After some trial-and-error and through observing the time development of the flooding potential after flooding has been switched on (as described below) we find that a flooding strength of $E_{\rm fl}=50\,k_BT$ results in an average value of the flooding potential of about $10\,k_BT$. We observe the typical behaviour that the system `feels' the flooding potential and within few picoseconds relaxes towards a slightly different structure, but still stays within the initial substate. This relaxation induces a drop of the initially large (about $25\,k_BT$) flooding energy down to the stable value of roughly $10\,k_BT$.

Taking this value as an estimate for the destabilization free energy $\Delta F$, we expect an acceleration factor of $e^{10}\approx 20\,000$. This seems to be a proper value, since the patch clamp experiments tell us that the gating proceeds on a time scale of several microseconds.

[Instead of this trial-and-error we could alternatively have used adaptive flooding (set switch to true) and directly enter the desired destabilization free energy of $10\,k_BT$. We will, however, not consider this further here.]

We thus chose to use a constant flooding energy of $E_{\rm fl}=50\,k_BT$and carry out the flooding simulation. The following control file ctl.lis is used:

33              Number of files.
shake.lis               
coord.lis               
...
forceout.lis            
2               Requested number of nodes.
353             Number of atoms.
1000            Freq. of analysis printout; next line is ...
A*
10              Frequency of writing restart file every analysis step!
0               Frequency of system call every analysis step.
ego2crd.sh
-50             Frequency of energy printout.
1000000         Number of integration steps.
1e-15           Integration time step in s.
5               Order of exclusion list.
FALSE           Switch for Minimisation.
1               Friction factor (1.0=>no friction, 0.0=>no motion).
0.08            Maximum position movement per integration step in A.
TRUE            Switch for Equilibration.
300             Target temperature in Kelvin.
1e-12           Coupling time constant in s.
8               Number of distance classes.
...
0               Used type of cluster algorithm (0 is default).
-2              Number of hierarchy levels.
-18             Number of branches on last level.
500             Frequency of reclustering.
out/            Path for output data.
0.4             Scaling factor for special 1-4 electrostatic damping.
TRUE            Switch for stochastic boundary.
TRUE            Switch for harmonic restraints.
TRUE            Switch for SHAKE on hydrogens (Only bond length).
...
TRUE            Switch for using flooding.
TRUE            Switch for using transl/rotation correction.
FALSE           Switch for using adaptive flooding.
50              Initial energy for flooding in kT.
50              Final energy for flooding in kT.
0               Flooding energy increase in kT/ps.
1e-12           Time constant for adaptive flooding in s.
0 0             Number of user defined integers and doubles.
END
0               DEBUG: 1 == compare with exact forces
0               DEBUG: only should be used by a developer.

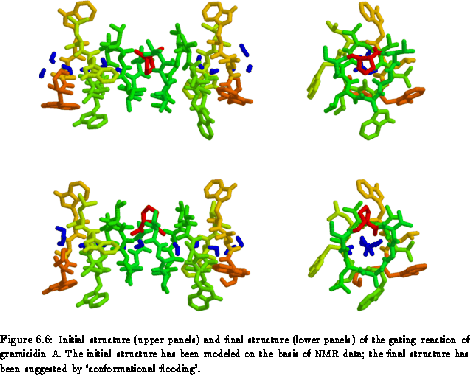
After about 100 picoseconds (the actually observed transition time is a stochastic quantity and, therefore, may vary considerably; it is distributed very much like decay times of individual radioactive atoms) we observe a sudden jump of the flooding energy to very small values, indicating the conformational transition we wanted to study. Indeed, inspecting the structure after this energy jump reveals the ring flip shown in Fig. 6.6.

The ego output files written during the drop of the flooding energy provide an approximate reaction path of the conformational transition. It can be used to calculate a free energy profile (e.g., with umbrella sampling techniques), which in turn provides a better estimate for the transition rate.

If the value for the flooding potential were chosen too small, e.g., $30\,k_BT$, no conformational transition would have been observed.

A very large value for the flooding potential can cause artificial deformations of the structure, which can be detected either by visual inspection or through a significant increase of the short-range energy contributions like `bond', `vdw', 'angle', or `dihedral'.

In rare cases it may happen that `conformational flooding' drives the system into a `dead end', i.e., a path starting with low free energies, which does not traverse an energy barrier, but rather ends at a barrier. In such a case the flooding energy will decrease significantly, but it will not drop down to very small values as in the case of a conformational transition. In most cases re-running the simulation with slightly different parameters (e.g., flooding strength) will help here. Alternatively, one can try to reduce the number of selected atoms in such a way as to focus more and more at those atoms involved in the transition. Note also that frequent `dead ends' can indicate that the value for the flooding strength has been chosen too large, and the system does not have enough time to `search' for a low energy pathway.

Always keep in mind:
The conformational motions you would like to see within a flooding simulations may be too slow as to be observed. Although we did not yet find any limit for the acceleration factor, it seems unlikely that transitions on the time scale of seconds can be accelerated by as much as nine orders of magnitude.

Finally:
Should you succeed in predicting a conformational transition using conformational flooding we would appreciate receiving a note from you.