


Next: Integration Methods
Up: Numerical Tasks in Molecular
Previous: Numerical Tasks in Molecular
In this section we review the computational aspects of molecular
dynamics simulations and discuss the relationship between the energy
function used by EGO and that used by the programs
CHARMM [3,4] and
X-PLOR [6], to which it is closely related.
Computer simulations of biological macromolecules are based on a
classical mechanical model of biomolecules. For the nuclei of the N atoms
of a molecule the Newtonian equations of motion
(
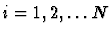 ) are assumed to hold
) are assumed to hold
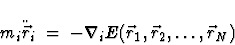
where  denotes the position of the i-th atom.
Here we have used the notation
denotes the position of the i-th atom.
Here we have used the notation
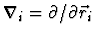 . The
function E
. The
function E 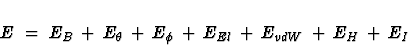
defines the total energy of the molecule. It is comprised of several
contributions which correspond to the different types of forces acting
in the molecule.
The first contribution, EB, describes the high frequency
vibrations along covalent bonds,
the second contribution,
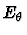 , the bending
vibrations between two adjacent bonds and
the third contribution,
, the bending
vibrations between two adjacent bonds and
the third contribution, 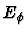 , the torsional
motions around bonds.
The fourth contribution, EEl, describes electrostatic
interactions between partial atomic charges, the charges being centered at
the positions of the atomic nuclei.
The next term, EvdW, accounts for the
van der Waals-interactions between non-bonded atoms in the molecule,
EH stands for the energy of hydrogen bonds,
and the last term, EI, describes so-called
improper motions of one atom relative to a plane described by three other
atoms. Various research groups have developed functional representations and
corresponding force constants which attempt to faithfully represent atomic
interactions and dynamic properties of
biomolecules [39,3,42,43].
The program which we have developed is based on the energy representation
of CHARMM [3,4]. Actually, our program can
read
, the torsional
motions around bonds.
The fourth contribution, EEl, describes electrostatic
interactions between partial atomic charges, the charges being centered at
the positions of the atomic nuclei.
The next term, EvdW, accounts for the
van der Waals-interactions between non-bonded atoms in the molecule,
EH stands for the energy of hydrogen bonds,
and the last term, EI, describes so-called
improper motions of one atom relative to a plane described by three other
atoms. Various research groups have developed functional representations and
corresponding force constants which attempt to faithfully represent atomic
interactions and dynamic properties of
biomolecules [39,3,42,43].
The program which we have developed is based on the energy representation
of CHARMM [3,4]. Actually, our program can
read![[*]](foot_motif.gif) a file of force parameters which has a format identical to that used by
X-PLOR [6], a simulation program closely related to CHARMM.
As a result, any adaptation of force constants suggested in the framework of
CHARMM or X-PLOR can be readily transferred to our program.
a file of force parameters which has a format identical to that used by
X-PLOR [6], a simulation program closely related to CHARMM.
As a result, any adaptation of force constants suggested in the framework of
CHARMM or X-PLOR can be readily transferred to our program.



Next: Integration Methods
Up: Numerical Tasks in Molecular
Previous: Numerical Tasks in Molecular
Helmut Heller
2000-04-19
![[*]](foot_motif.gif) a file of force parameters which has a format identical to that used by
X-PLOR [6], a simulation program closely related to CHARMM.
As a result, any adaptation of force constants suggested in the framework of
CHARMM or X-PLOR can be readily transferred to our program.
a file of force parameters which has a format identical to that used by
X-PLOR [6], a simulation program closely related to CHARMM.
As a result, any adaptation of force constants suggested in the framework of
CHARMM or X-PLOR can be readily transferred to our program.