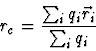
was derived, where
was derived, where
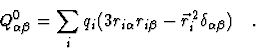
The Structure Adapted Multipole Method (SAMM) [33] takes advantage of knowledge about structural and dynamical features of biomolecules and helps to reduce the number of orders of multipole expansions for an approximate representation of the Coulomb potential. Large biomolecules are decomposed into small structural units. The electrostatic properties of these units can be approximated by their monopole or dipole moment. In our approach the force field generated by a group of atoms is approximated by an electrostatic monopole if the net charge does not equal zero (charged group of atoms), otherwise the force field is approximated by the dipole moment (dipolar group of atoms).
As the first non vanishing multipole moment does not
depend on the selected reference point, one can minimize the error used by
this approximation by selecting an optimal reference point.
In [33] for a charged group of atoms the optimal reference
point
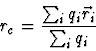
was derived, where ![]() denotes the sum over all atoms which belong
to the specified atom group. As a result of this optimization, the dipole
moment vanishes, and we effectively are accurate up to the dipole
moment. For dipolar units the optimal reference point
denotes the sum over all atoms which belong
to the specified atom group. As a result of this optimization, the dipole
moment vanishes, and we effectively are accurate up to the dipole
moment. For dipolar units the optimal reference point
![]()
was derived, where ![]() denotes the dipole moment
denotes the dipole moment
![]() .
The components of the quadrupole tensor
.
The components of the quadrupole tensor
![]() are given by
are given by
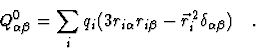
For a hierarchical treatment of electrostatic interaction these small structural units are grouped into larger aggregates -- we call such aggregates clusters -- at different levels of resolution. Usually EGO groups six structural units into a cluster, four clusters into a supercluster, and so on. In order to minimize the error of the electrostatic representation by the first non vanishing multipole moment, one has to maximize the compactness of the clusters. We want all clusters to have approximately the same size on every hierarchy level. This is a non trivial problem. In EGO a neural network algorithm for vector quantization [31] is used to solve this problem.
The FMM [20,29] uses a local Taylor expansion -- often called 'local expansion' -- of the electrostatic potential for every level of resolution to sum up forces generated by sufficiently far separated structural units or aggregates. In our implementation forces arising from atoms which are closer then about 10Å, called the innermost interaction zone (IIZ), are calculated exactly. In Figure 6.2 the interaction scheme of the Structure Adapted Multipole Method is illustrated. It shows how atoms, structural units and clusters contribute to the force acting on a selected atom.