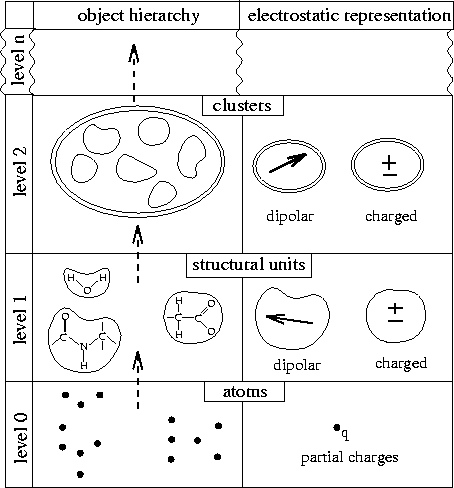
Figure: Structure adapted hierarchical description of biological macromolecules. Filled circles represent atoms, structural units are surrounded by a single-line border, and clusters are surrounded by a double-line border.
The SAMM method [19, 18, 26] exploits structural features of biomolecules to define a hierarchical grouping of partially charged atoms into local charge distributions, whose multipoles are subsequently used for evaluation of electrostatic interactions at large distances.

Figure: Structure adapted hierarchical description of biological macromolecules.
Filled circles represent atoms, structural units are surrounded by a
single-line border, and clusters are surrounded by a double-line border.
Figure 1 illustrates the hierarchy of charge distributions (``objects'') obtained by the SAMM-type grouping (left) and the electrostatic representations chosen for the resulting objects (right). Both, the definition of the objects and the choice of their electrostatic representations rest on the observation, that covalently bound atoms within biomolecules intrinsically form dynamically stable local groups, which either carry integer elementary charges or are uncharged, but dipolar. In case that the latter dipoles are small, the local groups are called non-polar and their electrostatics may be neglected [19, 18].
This observation suggests, that at larger distances the lowest multipole
moments of local groups can provide an accurate description of the
electrostatics within biomolecules.
Thus, charged local groups should be described by monopoles and dipolar
groups by dipoles for the description of their electrostatic interactions
at large distances.
In the SAMM method that
concept represents the guideline for the definition of the object
hierarchy illustrated in Figure 1.
As shown in the figure, at the bottom of the object hierarchy (level 0) no
local groups
are formed; instead individual atoms (filled circles) are considered as
the basic objects and are electrostatically represented by their partial
charges .
At small distances, i.e., at distances smaller than a predefined distance
.
At small distances, i.e., at distances smaller than a predefined distance
![]() , their interactions are evaluated by means of the Coulomb sum,
eq. (1).
For a description of electrostatic interactions at larger distances
covalently bound atoms are grouped into structural units
which are compact, typically include three to ten atoms, and form the first
level of the object hierarchy (level 1).
According to their respective electrostatic properties, SAMM distinguishes
three types of structural units:
``neutral units'' consist of uncharged atoms only; they need not be considered
and therefore are omitted in Figure 1.
``Dipolar units'', e.g., water molecules or peptide groups of a protein
backbone, are composed of partially charged atoms, exhibit a vanishing
net charge, and are represented by a dipole (arrow).
``Charged units'', e.g., charged side groups of amino acids, carry an integer
net charge and are represented by a monopole.
At all higher levels (level 2 and further up) pertaining to interactions at
still larger distances, i.e., at distances larger than a second, predefined
interaction distance
, their interactions are evaluated by means of the Coulomb sum,
eq. (1).
For a description of electrostatic interactions at larger distances
covalently bound atoms are grouped into structural units
which are compact, typically include three to ten atoms, and form the first
level of the object hierarchy (level 1).
According to their respective electrostatic properties, SAMM distinguishes
three types of structural units:
``neutral units'' consist of uncharged atoms only; they need not be considered
and therefore are omitted in Figure 1.
``Dipolar units'', e.g., water molecules or peptide groups of a protein
backbone, are composed of partially charged atoms, exhibit a vanishing
net charge, and are represented by a dipole (arrow).
``Charged units'', e.g., charged side groups of amino acids, carry an integer
net charge and are represented by a monopole.
At all higher levels (level 2 and further up) pertaining to interactions at
still larger distances, i.e., at distances larger than a second, predefined
interaction distance ![]() , objects of the preceding lower level
are grouped into clusters by means of self-organizing and adaptive vector
quantization techniques [49].
For a predefined number of clusters these techniques manage to minimize
cluster extension and, thereby, also the approximation error
caused by the truncation of the multipole
expansions [19, 18].
Depending on their total charge the clusters are represented
either by dipoles or by monopoles
, objects of the preceding lower level
are grouped into clusters by means of self-organizing and adaptive vector
quantization techniques [49].
For a predefined number of clusters these techniques manage to minimize
cluster extension and, thereby, also the approximation error
caused by the truncation of the multipole
expansions [19, 18].
Depending on their total charge the clusters are represented
either by dipoles or by monopoles .
We use
.
We use ![]() Å and
Å and
![]() Å for the interaction distances
associated with the hierarchy levels; that choice has been demonstrated to
guarantee highly accurate descriptions [19].
Å for the interaction distances
associated with the hierarchy levels; that choice has been demonstrated to
guarantee highly accurate descriptions [19].
Computationally the hierarchical multipole expansions of SAMM are defined and evaluated by a bottom-up scheme: The monopoles and dipoles of the structural units at level 1 are calculated from the individual charges of their enclosed atoms; at the second level the monopoles and dipoles of the clusters are obtained from the respective multipole moments of their embodied structural units and so forth; for further details see ref. [18].
Note that conformational changes in the protein or diffusive motions of solvent molecules would lead to an increase of cluster sizes in the course of an MD simulation, if the grouping of structural units into clusters would be chosen fixed. As a result, the accuracy of the electrostatic representation by the truncated multipole expansions would decrease. To maintain the accuracy of description SAMM periodically regroups the structural units into new clusters applying the adaptive techniques mentioned above. In principle, such regrouping represents a discontinuity of description and, thus, is a source of algorithmic noise. However, the chosen adaptive reclustering procedure assures, that the redistribution of structural units among clusters is kept minimal, and, therefore, also minimizes algorithmic noise [19, 18].
In addition to the diligent choice of structural units and of optimally compact clusters the SAMM method provides a further means to reduce the approximation error connected with the truncated multipole expansions, i.e., the choice of optimal reference points of the multipole expansions. This strategy is based on the fact that the first non-vanishing moment of a multipole expansion, in contrast to the higher moments, is independent of the reference point. As SAMM considers only the first non-vanishing moment, the truncation error can be made optimally small by an adequate choice of the reference point [19, 18].
Whereas the original version of SAMM [19]
solely comprises
a hierarchical multipole scheme, its enhanced version [26]
also utilizes FMM-strategies [23, 24].
Here, local Taylor expansions of the electrostatic
potential originating from distant charge distributions and their
associated multipole moments are used to speed up
the calculation of forces acting on partial charges in a given neighborhood.
A careful analysis of sample simulations has shown that the local Taylor
expansion may be safely truncated at second order, if the SAMM specific
distance classes are applied, i.e., if forces
originating from objects more distant than ![]() or
or
![]() are considered [18, 26].
Thus, the fast version of SAMM approximates the corresponding
electrostatic potential
are considered [18, 26].
Thus, the fast version of SAMM approximates the corresponding
electrostatic potential
![]() at position
at position
![]() ,
within the volume of a structural unit or cluster
in terms of its value and derivatives at the optimized reference
point
,
within the volume of a structural unit or cluster
in terms of its value and derivatives at the optimized reference
point ![]() of that object by the local Taylor expansion
of that object by the local Taylor expansion
![]()
where the expansion coefficients are defined by
![]()
In eqs. (2) and (3)
Greek indices enumerate Cartesian coordinates.
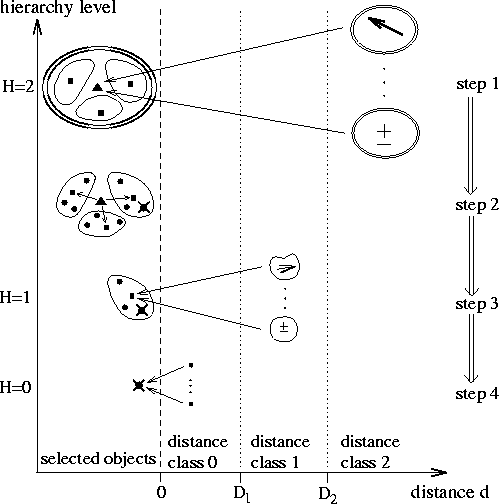
Figure: Illustration of algorithmic steps
connected with the local Taylor expansion
in the force calculation of the fast version of SAMM;
the contributions to the force on a selected atom
(![]() ) originating from
objects located within various distance ranges and associated to
corresponding hierarchy levels H are indicated by long arrows;
the reference points of the local Taylor expansions are denoted by triangles
(
) originating from
objects located within various distance ranges and associated to
corresponding hierarchy levels H are indicated by long arrows;
the reference points of the local Taylor expansions are denoted by triangles
(![]() ) for clusters (H=2) and by
squares (
) for clusters (H=2) and by
squares (![]() ) for structural
units (H=1); short arrows starting at a reference point indicate the
``inheritation of local Taylor expansions''; for explanation see text.
) for structural
units (H=1); short arrows starting at a reference point indicate the
``inheritation of local Taylor expansions''; for explanation see text.
Figure 2 illustrates the FMM aspect of SAMM
for the lowest three hierarchy levels, H=0,1,2.
As a function of object distance d it is shown how objects at different
hierarchy levels contribute (long arrows) to the electrostatic force
acting on a selected atom (![]() ).
Three corresponding distance classes
(
).
Three corresponding distance classes
(![]() )
are separated by vertical dashed lines. Within these distance classes
the figure displays those objects, which contribute to the force acting
on objects of the respective hierarchy level.
These objects, which contain the selected atom and which we correspondingly
call selected objects, are shown within the leftmost column.
For the evaluation of the total electrostatic force on the selected atom
the following algorithmic steps have to be performed in a top-down
fashion:
)
are separated by vertical dashed lines. Within these distance classes
the figure displays those objects, which contribute to the force acting
on objects of the respective hierarchy level.
These objects, which contain the selected atom and which we correspondingly
call selected objects, are shown within the leftmost column.
For the evaluation of the total electrostatic force on the selected atom
the following algorithmic steps have to be performed in a top-down
fashion:
The above presentation of the FMM-strategy utilized by SAMM completes the outline of that algorithm. We have seen how SAMM takes advantage of structural properties of protein-solvent systems and how this method exploits distance dependent spatial regularities of the corresponding electrostatic potential to construct a computationally fast and yet accurate approximation scheme.