Efficient MD-Simulation Methods

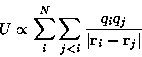
In order to solve the classical equations of motion numerically, and, thus, to obtain the motion of all atoms the forces acting on every atom have to be computed at each integration step. The forces are derived from an energy function which defines the molecular model [1,2,3]. Besides other important contributions (which we shall not discuss here) this function contains the Coulomb sum

$$U \propto \sum_{i}^{N} \sum_{j<i} \frac{q_i q_j}{\vert {\bf r}_i-{\bf r}_j \vert}$$

over all pairs of atoms (i, j) with partial charges q_i at positions ${\bf r}_i$. The evaluation of this sum dominates the computational effort in MD simulations as it scales quadratically with the number N of charged particles.

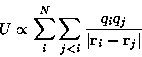
A very simple -- and in fact quite widely used -- approximation completely neglects long range electrostatic interactions beyond a certain cut-off distance [43] of typically 8-15Å. For systems which are significantly larger than this cut-off distance the computation of the remaining Coulomb interactions then scales with N instead of N². However, such truncation leads to serious artifacts concerning the description of the structure and dynamics of proteins [44,24,45], and more accurate methods which include the long range interactions should be preferred. Multipole methods and multiple-time-step methods are well established and widely used for this purpose. We briefly sketch both methods and subsequently show how their combination allows highly efficient simulations.