Efficient Multipole Methods

Multipole methods approximate the long-range forces originating from a group of point charges by truncated multipole expansions of their electrostatic potential. Using a hierarchy of grids for subdivision of space, nested at multiple scales, and a corresponding hierarchical organization of charge groups and multipole expansions [33] a computational complexity of O(N log N) can be achieved. By additionally using a hierarchy of local Taylor expansions for the evaluation of the electrostatic potential in the vicinity of a group of particles Greengard and Rokhlin have constructed the so-called fast multipole method (FMM) that even scales with O(N) for large systems [34,35].

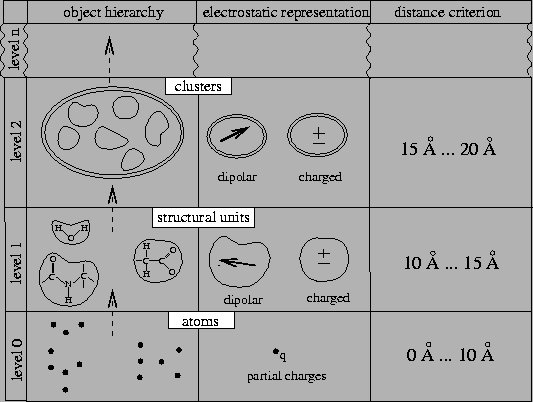
For MD simulations of biomolecules the FMM-type grouping of charges, defined by a fixed and regular subdivision of space, requires multipole expansions of rather high order (more than 6 terms of the expansion) as to achieve sufficient numerical accuracy [34]. If, instead, as shown in Figure 1, the charge grouping is adapted to specific structural and dynamical properties of the simulated biomolecules, the multipole expansions can be truncated at quite low orders, e.g., after the second order, while maintaining sufficient accuracy [36,37,38].

  

Figure: Structure adapted hierarchical description of Coulomb interactions in biological macromolecules. Filled circles (level 0) represent atoms, structural units (level 1) are surrounded by a single-line border, and clusters (level 2) are surrounded by a double-line border.

In the FAMUSAMM framework, e.g., we have grouped locally stable groups of typically three to ten covalently bound atoms into so-called structural units (level 1 in Fig. 1). By construction, these structural units either carry integer elementary charges or are uncharged, but dipolar. Test simulations show that for distances $>10\,$Å already the lowest non-vanishing multipole moments of these structural units provide a sufficiently accurate description of the electrostatic forces within biomolecules with an error below 2%. The objects of the next hierarchy level (level 2 in the figure) are formed by grouping structural units into clusters. For interaction distances $>15\,$Å the electrostatic potential of those objects, again, can be approximated by their lowest multipole moment. Extending this scheme to higher hierarchy levels, such a structure adapted multipole method (SAMM) provides a substantial speed-up for MD simulations as compared to the conventional, grid-based methods [38,46].

The performance of this first version of SAMM [36] can be further enhanced by additionally utilizing FMM-strategies [34,38]. Here, in the vicinity of a given object (e.g., a structural unit or a cluster) the electrostatic potential originating from distant charge distributions is approximated by a local Taylor expansion. Specifically, the basic tasks involved in the FMM aspect of SAMM are:

Task 1:

Calculate the first non-vanishing multipole moment of the electrostatic potential of composed objects (i.e., structural units and clusters).

Task 2:

Add up electrostatic potential contributions to local Taylor expansions of all objects on each hierarchy level. (Contributions to the local Taylor expansion of a selected object arise from all other objects on the same hierarchy which fulfill the distance criterion given in Fig. 1.)

Task 3:

Transform (``inherit'') local Taylor expansions from a upper hierarchy level to the next lower hierarchy level.

Task 4:

Explicitly calculate the Coulomb interactions between atoms which are closer than about 10Å.

In the next section we will illustrate how to further speed up the SAMM method by introducing multiple-time-stepping.