SAMM with Multiple-time-stepping

In general, multiple-time-step methods increase computational efficiency in a way complementary to multipole methods: The latter make use of regularities in space, whereas multiple-time-stepping exploits regularities in time. Figure 2 illustrates the general idea:

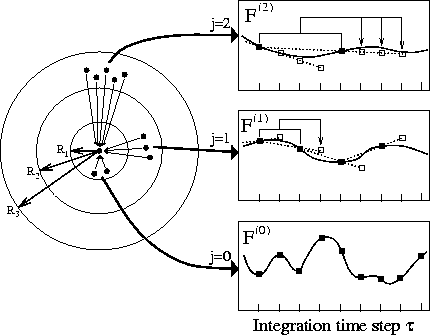
As sketched in the right part of the figure, forces between distant atoms generally exhibit slower fluctuations than forces between close atoms. Therefore, without significant loss of accuracy, the more slowly fluctuating forces may be computed using larger integration step sizes. As shown in the left part of the figure, the required classification of forces can be implemented, e.g., by grouping atom pairs into distance classes. The slowly fluctuating forces arising from outer distance classes may then be evaluated less frequently (filled squares) than the fast ones and, instead, are extrapolated (open squares) from previously computed forces at the time steps in between.

  

Figure: Distance classes $j=0,1,2,\ldots$ (left) are defined for an atom (central dot) by a set of radii R_j+1; the right curves sketch the temporal evolution of the total force ${\bf F}^{(j)}$ acting on the selected atom originating from all atoms in distance class j; shown are the exact forces (solid line), their exact values to be computed within the multiple time step scheme (filled squares), linear force extrapolations (dotted lines), and resulting force estimates (open squares).

This hierarchical extrapolation procedure can save a significant amount of computer time as it avoids a large fraction of the most time consuming step, namely the exact evaluation of long range interactions. Here, computational speed is gained at the cost of an increased demand for memory, e.g., for each atom and each distance class two previously computed forces have to be kept in memory.

In the framework of the fast structure adapted multipole method the memory demand could be drastically reduced. This was achieved by applying the multiple-time-step scheme (we used the so-called DC-1d scheme [24]) to the interactions between charge groups (structural units and clusters) rather than to the forces acting on individual atoms. In the following we give a short description of this tight and efficient combination. We termed the resulting algorithm FAMUSAMM (multiple-time-step structure-adapted multipole method)  [46,47].

A detailed analysis of fast SAMM has shown [47] that the most time consuming tasks are task 2 and task 4 described above. In task 2 for each hierarchy level (except for level 0) a local Taylor expansion is calculated for each object. Note that here we refer to expansions which comprise only contributions from objects of the same hierarchy level which, in addition, fulfill the distance criterion given in Fig. 1. From each of these local expansions, approximated electrostatic forces ${\bf\tilde{F}}^{(j)}$ acting on the atoms contained in the associated object could be computed and, in analogy to the exact forces ${\bf F}^{(j)}$ used in the multiple time step scheme described above (see Fig. 2), the multipole-derived forces ${\bf\tilde{F}}^{(j)}$ could be extrapolated by multiple time stepping. We further improved that obvious scheme, however, in that we applied multiple time step extrapolations to the coefficients of the local Taylor expansions instead. That strategy reduces memory requirements by a significant factor without loss of accuracy, since the number of local Taylor coefficients that have to be kept for the extrapolation is smaller than the number of forces acting on all atoms of the respective object.

Additionally, to optimize task 4, we applied a conventional, atom pair interaction based multiple-time-step scheme to the force computation within the innermost distance class. Here, for atom pairs closer than $5\,$Å, the Coulomb sum is calculated every step, and for all other atom pairs the Coulomb sum is extrapolated every second step from previously explicitly calculated forces.

This completes the outline of FAMUSAMM. The algorithm has been implemented in the MD simulation program EGO_VIII [48] in a sequential and a parallelized version; the latter has been implemented and tested on a number of distributed memory parallel computers, e.g., IBM SP2, Cray T3E, Parsytec CC and ethernet-linked workstation clusters running PVM or MPI.