 |
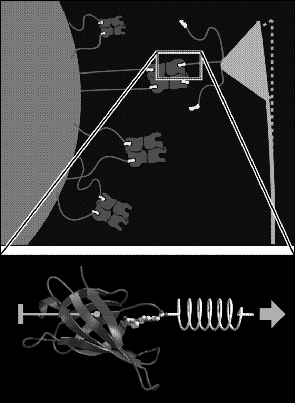
That simulation study [49] aimed at a microscopic interpretation of single molecule atomic force microscope (AFM) experiments [50], in which unbinding forces between individual protein-ligand complexes have been measured (Fig. 4, top). In particular we asked, what interatomic interactions cause the experimentally observed unbinding forces.
 |
Both the AFM rupture experiments as well as our simulation studies focussed on the streptavidin-biotin complex as a model system for specific ligand binding. Streptavidin is a particularly well-studied protein and binds its ligand biotin with high affinity and specificity [51]. Whereas previous experiments (see references in Ref. [49]) and simulation studies [52] referred only to bound/unbound states and the associated kinetics, the recent AFM rupture experiments have provided a new and complementary perspective on ligand binding by focussing at atomic details of binding/unbinding pathways: The former were described in terms of binding free energies as thermodynamic quantities, which are independent of the particular reaction pathway; the latter relate to forces, which actually depend on details of the unbinding reaction path and, therefore, can provide new insights into these details.
To enable an atomic interpretation of the AFM experiments, we have developed a molecular dynamics technique to simulate these experiments [49]. From such `force simulations' rupture models at atomic resolution were derived and checked by comparisons of the computed rupture forces with the experimental ones. In order to facilitate such checks, the simulations have been set up to resemble the AFM experiment in as many details as possible (Fig. 4, bottom): the protein-ligand complex was simulated in atomic detail starting from the crystal structure, water solvent was included within the simulation system to account for solvation effects, the protein was held in place by keeping its center of mass fixed (so that internal motions were not hindered), the cantilever was simulated by use of a harmonic `spring potential' and, finally, the simulated cantilever was connected to the particular atom of the ligand, to which in the AFM experiment the linker molecule was connected.
 |
However, one significant difference between the AFM experiment and its simulations cannot be avoided at present: Whereas the AFM experiment takes place at a millisecond time scale, our simulations had to be completed within the nanosecond time scale. So, in fact, in the simulation the pulling velocity had to be chosen about six orders of magnitude larger than in the AFM experiment!
In a first attempt to bridge these six orders of magnitude, we performed
a series of rupture force simulations using pulling velocities
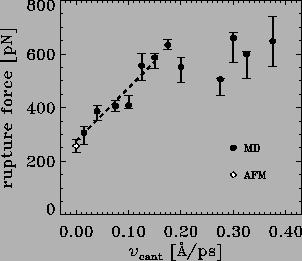
ranging from 0.375 to ![]() Å/ps. As can be seen in
Fig. 5,
we observed a linear dependency of the
computed rupture forces in the velocity range
between 0.15 and
Å/ps. As can be seen in
Fig. 5,
we observed a linear dependency of the
computed rupture forces in the velocity range
between 0.15 and ![]() Å/ps.
This suggests that
simple friction dominates the non-equilibrium effects in this regime
described by a friction coefficient of
Å/ps.
This suggests that
simple friction dominates the non-equilibrium effects in this regime
described by a friction coefficient of ![]() .
A simple linear
extrapolation of the computed rupture forces to the experimental time scale
shows agreement between theory and experiment.
Clearly, this first step has not yet solved the question how
to bridge the six orders of magnitude gap between theory
and experiment (cf. also [53]).
To answer that question, a better understanding of the physics
of rupture experiments using simplified models on the one hand
(cf., e.g., Ref. [54]) and, on the other hand, a careful
analysis of the atomic processes which cause the velocity dependent
rupture forces is necessary.
.
A simple linear
extrapolation of the computed rupture forces to the experimental time scale
shows agreement between theory and experiment.
Clearly, this first step has not yet solved the question how
to bridge the six orders of magnitude gap between theory
and experiment (cf. also [53]).
To answer that question, a better understanding of the physics
of rupture experiments using simplified models on the one hand
(cf., e.g., Ref. [54]) and, on the other hand, a careful
analysis of the atomic processes which cause the velocity dependent
rupture forces is necessary.
 |
One of the results of an MD rupture simulation is the
pulling force as a function of time or cantilever position
![]() ,
called the force profile. Figure 6 shows
an example, derived from an extended 1 ns-simulation, where a pulling
velocity of
,
called the force profile. Figure 6 shows
an example, derived from an extended 1 ns-simulation, where a pulling
velocity of ![]() Å/ps was used. The apparent multitude of force
maxima mirrors the complexity of the energy landscape traversed by the
biotin on its way out of the binding pocket. The peaks
of this force profile can be attributed to the rupture and formation
of individual hydrogen bonds and water bridges
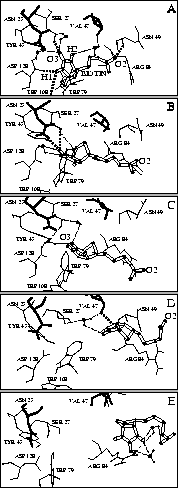
shown in the snapshots of Fig. 7,
which characterize the main steps of
the rupture process. The rupture forces in Fig. 5
are the maxima of the corresponding force profiles.
Å/ps was used. The apparent multitude of force
maxima mirrors the complexity of the energy landscape traversed by the
biotin on its way out of the binding pocket. The peaks
of this force profile can be attributed to the rupture and formation
of individual hydrogen bonds and water bridges
shown in the snapshots of Fig. 7,
which characterize the main steps of
the rupture process. The rupture forces in Fig. 5
are the maxima of the corresponding force profiles.
We will not discuss here in detail our atomic model of the unbinding process derived from our simulations and sketched in Fig. 7, but restrict ourselves to two unexpected features. One is that the rupture of the initially very strong hydrogen bonds between the ligand and the residues of the binding pocket (Fig. 7 A) does not entail immediate unbinding. Rather, the complex is stabilized by a transient network of water bridges and other transient hydrogen bonds, which form during the unbinding process (Fig. 7 B and C). Only after subsequent rupture of these hydrogen bonds the maximum force -- the rupture force -- is reached and the biotin rapidly moves out of the entry of the binding pocket (Fig. 7 D). As another feature we observed, towards the end of the unbinding process, a second force maximum, which we attribute to a strong transient hydrogen bond and several water bridges between biotin and the entry of the binding pocket (Fig. 7 E). Crossing of that second barrier, which cannot yet be resolved in the AFM experiment, completes the unbinding process.
In summary, our simulations provided detailed insight into the complex
mechanisms of streptavidin-biotin rupture. They attribute the binding
force to a network of hydrogen bonds between the ligand and the binding
pocket and show that water bridges substantially enhance the stability
of the complex.
Good agreement with experimental results was obtained.
Further `force simulations' of various systems, e.g., an antigen-antibody
complex, are in progress.
 |