Conformational Flooding

The previous application -- in accord with most MD studies -- illustrates the urgent need to further push the limits of MD simulations set by todays computer technology in order to bridge time scale gaps between theory and either experiments or biochemical processes. The latter often involve conformational motions of proteins, which typically occur at the microsecond to millisecond range. Prominent examples for functionally relevant conformational motions are the opening and closing of ion channels or, as proposed by Griffith [55] and Prusiner [56], pathogenic conformational transitions in prion proteins, the putative agents of mad cow and Creutzfeldt-Jacob diseases. Conformational motions often involve a complex and concerted rearrangement of many atoms in a protein from its initial state into a new conformation. These rearrangements, called conformational transitions, exhibit a multi-rate behaviour, which is is captured by the concept of ``hierarchical conformational substates'' introduced by Hans Frauenfelder [57]. According to that concept the free energy landscape of a protein exhibits a large number of nearly isoenergetic minima corresponding to the conformational substates, which are separated by barriers of different height [58].

  

Figure: `Conformational flooding' lowers free energy barriers of conformational transitions and thus accelerates such transitions. The figure shows a one dimensional cut through the high dimensional free energy landscape F (bold line) along a particular conformational coordinate c<sub>i</sub>. During an MD simulation the protein remains in the initial configuration (local minimum in the free energy), since the high barrier to the right cannot be overcome on an MD time scale. However, the MD simulation can serve to approximate the free energy harmonically in the vicinity of the initial configuration (dotted line) in order to derive an artificial `flooding potential' $V_{\rm fl}$ (dashed line). Inclusion of this potential (thin line) in subsequent MD simulations reduces the barrier height by an amount of $\Delta F$ and thereby destabilizes the initial configuration.

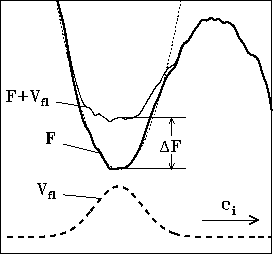
Figure 8 shows a one-dimensional sketch of a small fraction of that energy landscape (bold line) including one conformational substate (minimum) as well as, to the right, one out of the typically huge number of barriers separating this local minimum from other ones. Keeping this picture in mind the conformational dynamics of a protein can be characterized as ``jumps'' between these local minima. At the MD time scale below nanoseconds only very low barriers can be overcome, so that the studied protein remains in or close to its initial conformational substate and no predictions of slower conformational transitions can be made.

  

Figure: Two-dimensional sketch of the ${\rm 3N}$-dimensional configuration space of a protein. Shown are two Cartesian coordinates, x₁ and x₂, as well as two conformational coordinates (c₁ and c₂), which have been derived by principle component analysis of an ensemble (``cloud'' of dots) generated by a conventional MD simulation, which approximates the configurational space density $\rho$ in this region of configurational space. The width of the two Gaussians describe the size of the fluctuations along the configurational coordinates and are given by the eigenvalues $\lambda_i$.

In order to make such predictions possible, we have developed the conformational flooding (CF) method, which accelerates conformational transitions [59] and thereby brings them into the scope of MD simulations (``flooding simulations''). The method is a generalization of the ``local elevation method'' [60] in that it rests on a quasi harmonic model for the free energy landscape in the vicinity of the minimum representing the initial (known) conformational state. This model is derived from an ensemble of structures generated by a conventional MD simulation as will be described below and is shown in Fig. 9. From that model a ``flooding potential'' $V_{\rm fl}$ is constructed (dashed line in Fig. 8), which, when subsequently included into the potential energy function of the system, raises the minimum under consideration (thin line in Fig. 8) and thereby lowers the surrounding free energy barriers by an amount $\Delta F$ without severely modifying the barriers themselves. As a result, transitions over these barriers are accelerated by approximately the Boltzmann factor $\exp(\frac{\Delta F}{k_BT})$. In detail, the following steps are necessary to perform a CF simulation:

Step 1: A short conventional MD simulation (typically extending over a few 100ps) is performed to generate an ensemble of protein structures $\{{\bf x}\in {\cal R}^{3N}\}$ (each described by N atomic positions), which characterizes the initial conformational substate. The 2-dimensional sketch in Fig. 9 shows such an ensemble as a cloud of dots, each dot x representing one ``snapshot'' of the protein.

Step 2: This ensemble is subjected to a ``principal component analysis'' (PCA) [61] by diagonalizing the covariance matrix ${\bf C}\in \{{\cal R}^{3N}\times{\cal R}^{3N}\}$,

$${\bf C}:=\langle ({\bf x}-\bar{{\bf x}})({\bf x}-\bar{{\bf x}... ...ngle\quad \mbox{with}\quad \bar{{\bf x}}=\langle{\bf x}\rangle$$

i.e.,

$${\bf C}={\bf Q}^T{\bf\Lambda}^{-1}{\bf Q}$$

with orthonormal ${\bf Q}$ and ${\bf\Lambda}=(\delta_{ij}\lambda_i)\in \{{\cal R}^{3N}\times{\cal R}^{3N}\}$, where $\langle{\ldots}\rangle$ denotes an average over the ensemble $\{{\bf x}\}$.

Step 3: The eigenvectors of ${\bf C}$ define 3N-6 collective coordinates (quasi particles) , where we have eliminated the six rotational and translational degrees of freedom. From these 3N-6 degrees of freedom we select a number m<3N-6 conformational coordinates ${\bf c}=(c_1,\ldots,c_m)^T$ associated to the largest eigenvalues. Thus, the conformational coordinates cover most of the atomic fluctuations occurring at the 100 ps time scale. These m degrees of freedom are expected to dominate (not necessarily exclusively) conformational motion also at slower time scales [62,63,64].

Step 4: This PCA defines a multivariate Gaussian model $\tilde{\rho}^{{\bf c}}$,

$$\tilde{\rho}^{{\bf c}}({\bf c})\propto \exp\left[-{\bf c}^T{\bf\Lambda}_c{\bf c}/2\right]$$

of the conformational space density $\rho({\bf c})$, from which the quasi harmonic approximation of the energy landscape,

$$\tilde{F}({\bf c}) = -k_BT \ln\left[\tilde{\rho}({\bf c})\right] = \frac{1}{2}k_BT{\bf c}^T{\bf\Lambda}_c{\bf c}$$

is derived (see Ref. [59]).

Step 5: From that model of the current substate we construct the flooding potential $V_{\rm fl}$ of strength $E_{\rm fl}$,

$$V_{\rm fl} = E_{\rm fl} \hspace{2mm} \exp \left[ -\frac{1}{2}\frac{k_BT{\bf c}^T{\bf\Lambda}_c{\bf c}}{E_{\rm fl}}\right],$$

which is included in a subsequent MD simulation within the energy function used in the conventional MD simulation before (see Fig. 8), thereby causing the desired acceleration of transitions.

  

Figure: `Conformational flooding' accelerates conformational transitions and makes them accessible for MD simulations. Top left: snapshots of the protein backbone of BPTI during a 500 ps-MD simulation. Bottom left: a projection of the conformational coordinates contributing most to the atomic motions shows that, on that MD time scale, the system remains in its initial configuration (CS 1). Top right: `Conformational flooding' forces the system into new conformations after crossing high energy barriers (CS 2, CS 3, ...). Bottom right: The projection visualizes the new conformations; they remain stable, even when the applied flooding potentials (dashed contour lines) is switched off.

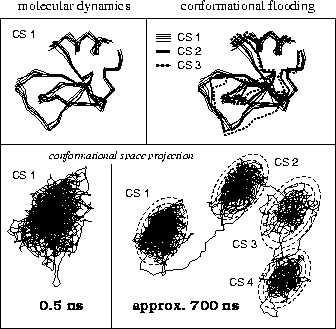As a sample application we describe simulations suggesting possible conformational transitions of the protein BPTI (Bovine Pancreatic Trypsin Inhibitor) at a time scale of several 100 nanoseconds (see Fig. 10). First we carried out a conventional MD simulation of 500 ps duration (no explicit solvent included), during which the protein remained in its initial conformational substate CS 1. The upper left part of the figure shows several snapshots of the backbone taken from that simulation; the lower left shows a projection of the 500 ps trajectory onto the two conformational coordinates with largest eigenvalues (corresponding to Fig. 9). From that ensemble we constructed a flooding potential as described above (dashed contour lines, superimposed to the CS 1-trajectory, bottom right). The flooding potential was subsequently switched on and rapidly induced a conformational transition (to the right in the figure) into another energy minimum, CS 2. After switching off the flooding potential the new conformational state of the protein remained stable, indicating that, indeed, the new minimum is separated from CS 1 by a large energy barrier. Using multi-dimensional transition state theory [59] we could estimate that in an conventional (i.e., unperturbed) MD simulation that conformational transition would have been observed only after several hundred nanoseconds. As shown in Fig. 10, the CF method can be applied iteratively to systematically search for further conformational substates, CS 3, CS 4 etc. The upper right part of the figure shows the backbone configuration of BPTI corresponding to the new substates.

MD simulations are valuable tools if one wants to gain detailed insight into fast dynamical processes of proteins and other biological macromolecules at atomic resolution. But since conventional MD simulations are confined to the study of very fast processes, conformational flooding represents a complementary and powerful tool to predict and understand also slow conformational motions. Another obvious application is an enhanced refinement of Xray- or NMR-structures.