Long time observables

As to investigate the influence of approximation schemes on the description of protein structure and dynamics we first analyze the temporal evolution of the rms deviations defined by eq. (8). The graphs shown in Figure 5 have been obtained from the various 1.2ns simulations of BPTI in vacuo. The graphs represent smoothened versions of obtained by taking local averages of 5ps width.

  
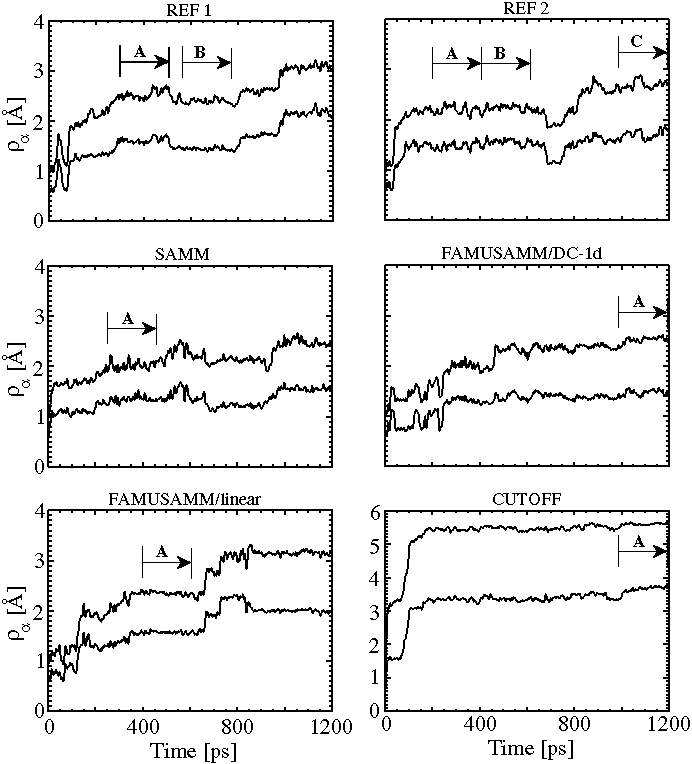
Figure 5: Temporal evolution of backbone rms deviations and side chain rms deviations for the two reference simulations (REF1 and REF2) and the four approximation methods; due to the flexibility of the side chains, is always larger than ; trajectory sections, which correspond to stable substates and are used for later evaluation of the covariance matrices, are denoted by capital letters; for explanation see text.

The rms deviations of the side chain atoms are always larger than the rms deviations of the backbone atoms, since side chains are much more flexible than the protein backbone. As can also be seen in Figure 5, both and increase with simulation time and generally exhibit a series of jumps. The first jump reflects the thermal fluctuations around the initial structure, whereas later jumps, as shown by a closer inspection of the associated structures (data not shown), arise from conformational transitions.

Furthermore one recognizes from the top two plots in Figure 5 that the time development of the rms deviations distinctly differs for the two reference simulations indicating that, indeed, the chaotic character of the system has led to a complete decorrelation of the respective trajectories. Yet the rms deviations resulting after 1.2ns are of similar size and measure Å and Å respectively. Within the first 200ps our rms deviations agree well with those obtained from other BPTI simulations in vacuo of up to 210ps length [6, 2].

Inspection of the subsequent three plots in Figure 5 shows that for SAMM and FAMUSAMM the overall behavior of is similar to that obtained for the two reference simulations. All graphs exhibit jumps pointing towards conformational transitions, and after 1.2ns the values of are close to those of the reference simulations.

In contrast, exhibits a qualitatively and quantitatively different behavior for the cutoff simulation (lower right plot; note the different scale). Here one single and large conformational transition occurs after about 100ps, and subsequently conformational transitions are suppressed. As shown by an analysis of the proteins structure, the transition was connected with a contraction upon which its overall size shrank by about 5Å.

In summary, as monitored by , no essential differences can be detected between the reference simulations, SAMM, and FAMUSAMM simulations, whereas the cutoff simulation apparently describes a different system.

We now turn to the investigation of dynamical correlations as described by the covariance matrices defined in eq. (9). As noted above, a comparison of such matrices requires that the trajectories, from which the are calculated, refer to identical or at least similar conformational substates of the protein. Inspection of Figure 5 shows that one can identify a couple of sections within the trajectories of the simulations pointing to conformational substates which are stable for at least 200ps. These sections marked by capital letters in Figure 5 were employed for evaluation of associated covariance matrices.

Differences between the covariance matrices calculated in this way can be due to various sources: (i) they may represent pure statistical fluctuations, (ii) they may reflect dynamical variations associated with the individual conformational substates, and (iii) they may be caused by the application of deviating computational methods.

In order to disentangle these sources we first provide an estimate for (i) the size of statistical fluctuations. For that purpose we chose the two consecutive 200ps sections of the second reference trajectory, which are marked in Figure 5, top right, as A and B. As is indicated by the constancy of the in that period, these sections refer to one and the same conformational substate of BPTI. Figure 7(a) shows an overlay of the two covariance plots calculated from the covariance matrices associated with these trajectory sections and displays the value of the rms difference between the covariance matrices.

  
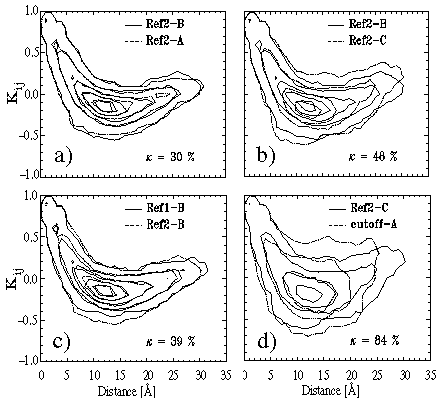
Figure: Covariance plots for comparison of BPTI dynamics within stable conformational substates simulated by different methods (see text for explanation).

As one can see, the two plots are nearly identical. They show strong positive correlations between motions of neighboring atoms, which reflect the rigidity of the covalently bonded structure. At intermediate distances around Å anti-correlations dominate, whereas correlations become positive again at distances larger than Å. The rms deviation of the two cross correlations is %. Thus deviations have to be distinctly larger than that value, and covariance plots have to exhibit much more pronounced differences than those in Figure 7(a), as to exclude mere effects of statistical fluctuations and to prove the existence of physical or algorithmic differences of the simulated dynamics.

A measure for the alteration of correlations of atomic motion, which is induced by a conformational transition into a different substate [see point (ii)], is provided by Figure 7(b). This figure also shows covariance matrices extracted from the second reference trajectory, but in contrast to Figure 7(a) trajectory sections referring to different substates of BPTI are compared. Specifically, sections B and C as marked in Figure 5, top right, have been chosen for comparison. In comparison to Figure 7(a), the covariance plots exhibit sizable differences, and the rms deviation of cross correlations, measuring %, is larger. But note that, apparently, the conformational transition from state B to state C has had little influence on the overall shape of the covariance plots.

Similar conclusions may be drawn, if one considers Figure 7(c). This figure compares covariance plots extracted from different trajectories calculated with the same computational method, i.e., sections B of the first reference simulation and section B of the second reference simulation as marked in Figure 5, top plots. These sections refer to slightly different substates, which have been selected according to a criterion of maximal structural similarity. Consequently, the good match of the covariance plots in Figure 7(c) as well as the low value of % indicates that closely resembling structures exhibit similar dynamics.

In order to finally pin down the range within which the rms deviations of cross correlations can vary upon conformational transitions at a nanosecond time scale, we have additionally selected a whole set of 200ps sections corresponding to stable substates from the two reference trajectories. We found that never exceeded 70% and had a mean value of 58%.

We now are in a position to use our long time observables as to distinguish algorithmic artifacts from effects of statistical fluctuations and conformational transitions. For this purpose we will select from the trajectories calculated with the approximate methods 200ps sections with the following properties: (a) They should refer to stable substates, and (b) the structure of that substate should be as similar as possible to the structure of one of the substates sampled in one of the reference trajectories.

Figure 7(d) clearly indicates that the cutoff method is prone to algorithmic artifacts concerning the description of dynamics. This conclusion is validated in particular by the large value of 84% for the rms deviation , which, in contrast to the covariance plot, solely expresses dynamical properties; note that the contour plots additionally display distance information.

  
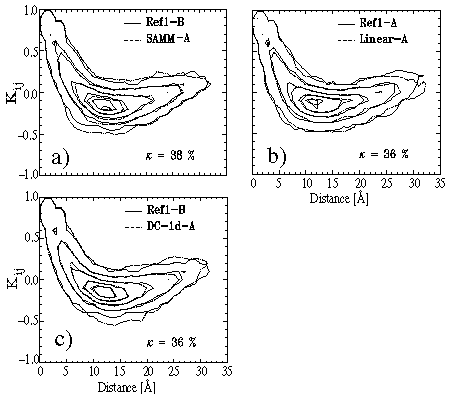
Figure: Further covariance plots for evaluation of our simulation methods.

Quite in contrast to the cutoff method all approximate methods, which account for long range Coulomb interactions by structure-adapted multipole expansions, show excellent performance in our test on dynamics. This statement is proven by Figure 8 displaying the respective covariance plots and the values of . As monitored by the plots and by , in all cases the substate dynamics calculated by SAMM and FAMUSAMM resembles quite closely to the dynamics of a similar substate sampled by the reference simulations. The comparisons are as close as those between the sections B of the reference simulations shown in Figure 7(c). Furthermore we have also selected a set of 200ps sections referring to arbitrary substates from the SAMM and FAMUSAMM trajectories for comparison with substate sections from both reference simulations using as the observable. Like in the comparison among the reference sections noted further above, no value larger than 70% was found for . As a consequence, concerning dynamics, no difference has been detected between the exact evaluation of long range Coulomb forces and our approximate methods.

Summarizing the results of our study on the accuracy of the various approximate MD algorithms we may state, that the FAMUSAMM/DC-1d algorithm (a) provides forces which are nearly as accurate as those obtained with SAMM, (b) entails only comparable little algorithmic noise, and (c) passes also our tests on the description of protein structure and dynamics with equally excellent results. In contrast, FAMUSAMM/linear is hampered by pronouncedly increased algorithmic noise, whereas the cutoff method exhibits unsatisfactory behavior in every respect. In view of these results we have discarded the linear multiple-time-step extrapolation scheme from further consideration within FAMUSAMM. It remains to be checked, to what extent the favorable algorithmic properties of FAMUSAMM are accompanied by a correspondingly favorable computation performance.