Before starting with the detailed outline of our FAMUSAMM method we want to annotate on an important progress concerning its implementation as compared to that of SAMM: The first two SAMM versions [19, 18, 26] made use of only two hierarchy levels, which restricted their applicability to medium-sized systems comprising less than about 5,000 atoms. To gain substantial speed-ups also for larger systems, we decided for the design of FAMUSAMM to implement a fast SAMM method with an arbitrary number of hierarchy levels. That number is now determined by the number of atoms in a given simulation system and is chosen automatically in the start-up phase of a simulation [50].
a) Basic concepts
Our FAMUSAMM algorithm has been designed to further reduce the computational
effort for the evaluation of Coulomb
forces by exploiting regularities of these forces
in space and time.
The basis of its development has been the identification of the most
time-consuming steps within the fast SAMM algorithm.
Only upon such an analysis one may expect that a combination with a
multiple-time-step method can render additional speed-ups:
A detailed inquiry of fast SAMM has shown [50],
that the essential time consuming steps are (i) the calculation of
contributions to the local Taylor expansions
(see Figure 2, steps 1 and 3)
and (ii) the calculation of the electrostatic forces for the innermost
distance class (see Figure 2, step 4).
Therefore, we have focused our efforts on these two steps.
b) Multiple-time-step extrapolation of local Taylor expansions
First consider step (i) and remember, that the
hierarchy of interactions, which is employed for the evaluation
of the local Taylor expansions and is depicted in
Figure 2, is defined by a hierarchy of distances.
This hierarchy of distances is intimately related to the particular concept
of distance classes underlying the multiple-time-step schemes as discussed
above. Therefore, an attempt to combine these methods seems natural:
In multiple-time-step methods the total force 
acting
on a selected atom originating from distance class j is extrapolated.
Since we now want to use a multipole method, we have to identify a
corresponding expression for this force.
As we have seen in our outline of the SAMM algorithm,
the total force originating from outer distance
classes and acting on elements contained in a
cluster or a structural unit is computed by means of a local Taylor expansion.
Such a local Taylor expansion for an object on a given hierarchy level
is -- except for the topmost level -- made up of two components:
(a) a contribution inherited from the next higher
hierarchy level (see Figure 2, step 2) comprising
the electrostatic interactions with objects in all outer distance classes, and
(b) contributions from objects within the same hierarchy level.
From the latter one can calculate the desired total force
and,
therefore, we apply multiple-time-step extrapolations to these contributions.
Here, instead of extrapolating the forces directly, we extrapolate
the coefficients 
,
and
of the local Taylor expansions, from which the forces derive
.
c) Inner class force extrapolation
Because of the choice of 10Å for the interaction distance
rendering
quite a few, typically about 400, interaction partners for a given
partial charge within the innermost distance class (H=0) of SAMM,
the second essential time consuming step (ii) of that method
is the calculation of electrostatic forces by the Coulomb sum,
eq. (1).
In fact, this step is equivalent to the one carried out in conventional
truncation methods using a cut-off distance .
To reduce that effort by application of a multiple-time-step method, we
split this SAMM distance class into two new distance classes
j=0 and
j=1 with the respective radii
Å and
Å.
Within these new distance classes we extrapolate forces directly by a
multiple-time-step scheme as described in the section before.
Distance classes of similar size have been successfully used
previously [16].
Due to the introduction of these new distance classes, the expensive computation of about 400 interactions per particle is now performed only at every second integration time step, whereas in distance class j=0 only a few interactions, about 50, have to be evaluated at every integration step. Hence, the overall computational effort for the innermost SAMM distance class is reduced nearly by a factor of two.
d) Interaction list updates
Generally, MD methods, which are based on distance classes, use
interaction lists to eliminate the need for time consuming interaction
partner searches at each integration time step [32].
In FAMUSAMM that strategy is adopted as follows:
For each object at a particular hierarchy level (atom, structural unit, cluster)
an associated interaction list points to
all objects, which belong to the same hierarchy level and meet
the distance criterion described above (cf. Figure 2).
Because distances between atoms, structural units and clusters vary
during an MD simulation, the interaction lists have to be updated from time
to time and are likely to change upon these updates.
As a result, the forces generated by changing numbers of objects within a
given distance class will change discontinuously.
The reclustering procedure of SAMM mentioned above causes similar
discontinuities.
However, the occurrence of such discontinuities disables the application of
multiple-time-step extrapolation procedures, since the latter are based on
strict smoothness assumptions:
Only if the interaction lists and cluster compositions
are kept fixed for a sufficiently large [
, see subsection f)] number
of integration time steps, multiple-time-step extrapolations may be applied.
Test simulations have shown, that for our FAMUSAMM interaction lists
update periods covering up to 128 integration steps can be used;
reclustering periods may be even longer and are chosen as integer
multiples of the former periods.
e) Verification of local Taylor expansion smoothness
As described above, an essential new feature of FAMUSAMM as compared to
previous multiple-time-step schemes is the extrapolation of
local Taylor expansion coefficients for outer distance classes instead
of the extrapolation of forces acting on individual atoms.
To verify the validity of this approach it remains to be checked, whether
the smoothness conditions required for multiple-time-step extrapolations
actually hold for the local Taylor expansion coefficients.
Extended test simulations have demonstrated, that this is the case, indeed,
and that local Taylor expansion coefficients exhibit decreasing amplitudes
and curvatures with increasing hierarchy level H.
f) Initialization
A prerequisite for the application of the multiple-time-step extrapolation
at a given time step in a simulation is the accessibility to two
previously explicitly calculated forces or local Taylor expansion coefficients.
As these are absent in the start-up phase of a simulation or,
due to the associated discontinuities, cannot be used after an update of
the interaction lists, special precautions have to be taken for
these periods [32].
To be specific, the extrapolation of forces or of local coefficients for
distance class j requires their values at two previous macro
integration steps which are separated by 
basic integration steps
(see Figure 3).
To provide these values for the initialization periods FAMUSAMM performs
exactly 
conventional fast SAMM steps until all necessary
forces (for j=1) or local coefficients (for
) are explicitly
calculated.
Obviously, the initialization periods, after which multiple-time-step
extrapolations can be applied, have different durations 
for the
various distance classes.
For the computationally most expensive distance classes,
j=1 and
j=2, the initialization
lasts only 2 and 4 integration steps, respectively.
From these numbers it is clear that the efficiency loss due to the
initialization phases is negligible, if periods of 64 or
more steps are used for the update of the interaction lists.
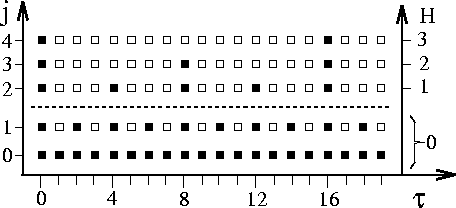
Figure 4: Extrapolation scheme of FAMUSAMM; 
denotes the integration step,
H the SAMM hierarchy level and
j the multiple-time-step distance class;
filled squares mark the integration steps at which forces
originating from objects in
distance class j are explicitly calculated,
whereas empty squares indicate computationally inexpensive extrapolations.
The dashed lines separate the regime of force extrapolation in distance
class j=1
(H=0) from the regime of local Taylor expansion
extrapolation in the outer distance classes
(
);
forces originating from partial charges in the innermost distance class j=0
are never extrapolated.
g) The FAMUSAMM algorithm
Figure 4 illustrates the multiple-time-step scheme of
FAMUSAMM by which long range Coulomb interactions are evaluated.
For a simulation period well after an initialization phase three
hierarchy levels H and a sequence of
20 integration
steps are shown.
Filled squares indicate explicit fast SAMM force calculations, empty squares
extrapolations.
The dashed line separates the
Coulomb sum interaction classes (j=0,1) from distance classes
which interact by multipole expansions ().
For class j=1 the extrapolation of forces is used, i.e.,
the respective forces are evaluated only at every second integration step
and are extrapolated otherwise;
whereas, the electrostatic interactions of partially charged atoms closer
than Å (see Figure 3,
j=0)
are calculated at every integration step.
For distance classes , which correspond to hierarchy levels
, the multiple-time-step scheme is applied to the
local Taylor expansion coefficients.
Here, the local Taylor expansion coefficients of lower
hierarchy levels have to be recalculated more often than those
of higher hierarchy levels, which, in turn, can be extrapolated more often.
As suggested in a previous multiple-time-step method [16],
explicit recalculation is performed every
-th integration step.
Appendix A summarizes the FAMUSAMM algorithm using a pseudo-code description. The algorithm has been implemented in the MD simulation program EGO_VIII [51] in a sequential and a parallelized version; the latter is suited for distributed memory parallel computers, e.g., IBM SP2, Cray T3D, Parsytec CC and workstation clusters under PVM or MPI. Details on the parallelization strategy will be given in a forthcoming publication [52].
As is apparent from the large number of empty squares depicted in Figure 4 FAMUSAMM replaces quite a few explicit force or local Taylor expansion calculations by extrapolations for the sole purpose of computational efficiency. As noted already in the introduction, in MD-simulations the inaccuracies associated with these FAMUSAMM approximations may effectively act as sources of uncontrolled algorithmic noise. It is the aim of the remaining sections of this paper to check, to what extent such numerical artifacts can affect the MD description of structural and dynamical properties of proteins.